Trainings-Tipps | -Anleitungen | -Hilfen | -Ideen
Hier findest du passende Anregungen, um deine Fertigkeiten im Umgang mit der Kugel möglichst variantenreich und damit ganzheitlich zu trainieren.
… trainieren heißt allerdings: Tu auch was und lies nicht nur… es bedeutet schon Arbeit – „Von nix kommt …“!
Knobelaufgaben
… als ein kleiner Baustein mentalen Trainings
Man kann Willensstärke trainieren
Mentaltraining ist ein Zauberwort – hat mit Zauberei allerdings absolut nichts zu tun.
Mentales Training bedeutet auch keineswegs, dass irgendjemand mit dem Finger schnippt und schon ist ein „Problem“ keines mehr.
Mentaltraining ist Arbeit mit und durch das eigene Gehirn.
Knobelaufgaben und Rätsel sind eine gute Möglichkeit, das eigene Gehirn mit neuen Herausforderungen zu belasten und zu trainieren – eine Form mentalen Trainings.
Viele Knobelaufgaben und knifflige Rätsel sind in ihrer Formulierung so gestaltet, dass man nur indirekt auf die richtige Lösung kommt. Das Gehirn muss unter Umständen mehrere Umleitungen nehmen bis es sich zurechtfindet.
Intelligenz oder gar explizites mathematisches/physikalisches Talent spielt hierbei eigentlich kaum eine Rolle.
Kreatives und assoziatives Denken wird bei den gestellten Aufgaben gefördert und auch geschult.
Der Spaß bei Denk- und Knobelaufgaben ist hierbei nicht nebensächlich, sondern gewollt.
Denk- und Knobelaufgaben
(Die jeweiligen Lösungen gibt´s immer weiter unten)
Begriffserkärungen nach Wikipedia | Rätsel / Laterale
Wikipedia (die freie Enzyklopädie)
Ein Rätsel ist eine Aufgabe, die durch Denken gelöst werden muss.
Rätsel können dem Zeitvertreib, der Unterhaltung und der Bildung des Rätsellösers dienen.
Ihre Lösung wird teilweise durch irreführende, mehrdeutige Angaben erschwert. Schwierig zu lösende Rätsel werden redensartlich auch als Knacknuss oder Kopfnuss bezeichnet, da sie einer Nuss ähnlich „schwer zu knacken“ sind.
Ein Lateral ist ein Rätsel, bei dem mit wenigen Informationen eine paradox oder unsinnig erscheinende Endsituation einer Kurzgeschichte vorgegeben wird, deren vorheriger Verlauf durch gezieltes Nachfragen gefunden werden muss.
Ein Lateral wird manchmal auch (etwas ungenau) als Ja-Nein-Rätsel bezeichnet.
Da sehr oft eine kriminelle Geschichte zugrunde liegt, ist auch die Bezeichnung Rätselkrimi geläufig.
Denkt erst mal nach und setzt euren Ehrgeiz ein ...
… , um die Aufgaben zu meistern!
Schreit nicht gleich (bequem und feige) nach den Lösungen, die euch natürlich die eigene (Kopf-)Arbeit der Lösungssuche abnehmen.
Konzentriert euch und gebt nicht auf.
Ihr seht:
Es sind genau DIE Eigenschaften, die ein/e gute/r Pétanque-Spieler/in braucht.
Also genau das richtige Training für daheim – Bequemer geht´s doch eigentlich kaum?!
47 | Wachsverschwendung beim jährlichen Adventskranz
Jedes Jahr kann man sich zur Vorweihnachtszeit über die Kerzenverschwendung auf dem Adventskranz ärgern:
Am ersten Advent wird eine Kerze angezündet, am zweiten zwei, am dritten drei und am vierten vier Kerzen.
Vollständig abbrennen wird -wenn überhaupt- nur die erste Kerze – die anderen Kerzen haben im Vergleich zu den jeweils vorhergehenden viel zu wenig „Brennzeit“ zur Verfügung – Wachsverschwendung.
Ein pfiffiger Sparer nimmt sich dieses Problems nun an und stellt in diesem Jahr seine Adventskerzen selbst her und schmilzt sie jeden Sonntag wieder ein.
Aus dem flüssigen Wachs gießt er vier gleich große Kerzen für den nächsten Advent. Am vierten Advent sollen alle vier Kerzen nach einer Stunde vollständig abgebrannt sein.
Eine Kerze von 100 Gramm kann genau vier Stunden lang brennen.
Der pfiffige Sparfuchs zündet die Kerzen an jedem Advent für genau eine Stunde an.
Wie viel Wachs braucht er dafür?
46 | Ganz schön verdreht
68 – 88 – X – 98
Was ist X?
45 | Welche Zahl ist gesucht?
Welche Zahl ist gesucht – Wer kann die Gleichung und das Rätsel lösen?
Eine sehr interessante Knobelaufgabe mit mehreren Zahlen und Gleichungen.
Gerüchten zufolge
kann das Problem von kleinen Kindern durchschnittlich in 5-10 Minuten herausbekommen werden.
Mathematiker und Programmierer lösen die Aufgabe in etwa einer Stunde und Menschen mit besonders hohem Bildungsstand… naja probiere es selbst aus!
Viel Spaß beim Knobeln!
7890 = 4 3664 = 3
3700 = 2 3678 = 3
1111 = 0 0000 = 4
5890 = 4 1111 = 0
2630 = 2 1890 = 4
3859 = 3 7801 = 3
1462 = 2 8880 = 7
8444 = 5 2580 = ???
44 | Was für eine Frage?
Ein Mann sagt zu einem anderen:
„Ich werde Dir eine Frage stellen, auf die es eine eindeutig richtige Antwort gibt – entweder ja oder nein -, aber es wird Dir unmöglich sein, meine Frage zu beantworten.
Möglicherweise wirst du die richtige Antwort kennen, aber du wirst sie mir nicht geben.
Jeder andere wäre vielleicht in der Lage, die Antwort zu liefern, du aber nicht.“
Welche Frage wird er ihm stellen?
43 | Rätselhafte Addition - Buchstaben ersetzen
Ersetze die Buchstaben in der folgenden Additionsaufgabe durch die richtigen Zahlen.
Bedenke: Gleicher Buchstabe = gleiche Zahl!
S E N D
+ M O R E
————
M O N E Y
Und (für die ganz Fleißigen) noch eine Buchstaben-Addition:
FORTY
+ TEN
+ TEN
——-
SIXTY
42 | Welches Wort passt nicht?
Welches Wort passt nicht zu den andern?
1: R) abgeben S) ausschütten T) abholen U) weglegen
2: D) unbeholfen E) unpassend F) ungeschickt G) tollpatschig
3: B) Spass C) Glück D) Freude E) Vergnügen
4: E) nutzlos F) unbrauchbar G) ungeeignet H) hoffnungslos
5: L) Freude M) Angst N) Gefahr O) Ärger
6: I) übertreiben J) betonen K) herausstellen L) hervorheben
7: H) Kranz I) Babeli J) Säuli K) König
Die Lösungsbuchstaben ergeben in der Reihenfolge 1 – 7 ein Wort.
Wie heisst es?
41 | Das Verwandtschaftsproblem
Sie kommen mit einem Pärchen – einem Mann und einer Frau – ins Gespräch.
Nachdem Sie sich vorgestellt haben, wollen Sie wissen, wie die beiden zueinander stehen.
Die Frau gibt Ihnen folgenden Hinweis: „Seine Mutter ist meiner Mutter Schwiegermutter!“
Wie sind die beiden miteinander verwandt?
40 | Warum stutzt er, als er die Frau im Tea Room sieht?
(Rätselkrimi von Roger Graf)
Mein Herz schlug heftig, als ich den blauen Mantel abtastete. In der rechten Manteltasche fand ich, was mein Diebesherz am meisten beglückt: ein prall gefülltes Portemonnaie. Die restlichen Jacken tastete ich im Eilverfahren ab. All das dauerte nicht mal zwei Minuten. In einem Innenhof machte ich es mir neben einer Mülltonne gemütlich. Manchmal gelang es mir, mit einer Bankomatkarte Geld abzuheben, weil der Besitzer oder die Besitzerin den Code der Karte ins Adressbuch geschrieben hatte. Diesmal begnügte ich mich mit den 400 Franken, die ich im Portemonnaie fand. Die Ausweise und Kreditkarten wollte ich in die Mülltonne werfen, so wie ich es immer tat. Doch diesmal fiel mein Blick auf die Identitätskarte, und im gleichen Moment war es um mich geschehen. Ein geheimnisvoll lächelndes Gesicht, umspielt von langen gelockten Haaren, schaute mir entgegen. Eine Ewigkeit verging, bis ich wieder richtig denken konnte. Unbekannte Schöne Nur weg von hier. Doch im Innenfach des Portemonnaies stieß ich auf zwei Fotos. Sie zeigten die gleiche Frau, an einen Stehtisch lehnend, in der linken Hand eine Zigarette – was für ein Anblick! Ich war trunken vor Glück, und wie ein Betrunkener wusste ich später nicht mehr, wie ich nach Hause gekommen war. Ich wusste nur, dass ich diese Frau kennen lernen musste. Es ging nicht anders. Ich sah sie, wie sie das Haus verließ, in dem sie wohnte – dritter Stock links. Tagsüber arbeitete sie in einer Bank, sie trug elegante Kleider, unterhielt sich mit glattrasierten jungen Männern, die alle aussahen wie Eigenheimbesitzer in den Werbespots. Abends legte sie die strenge Kleidung ab und ging in Jeans und einem Schlabberpulli in die Schule für Erwachsene, wo sie Kurse in Englisch und Französisch besuchte. Nach der Schule ging sie, oft wieder in eleganter Kleidung, mit teure Autos fahrenden Männern essen. Doch fast immer kehrte sie allein in ihre Wohnung zurück. Ganz allein war sie nie. Ich war jetzt immer in ihrer Nähe, lebte vom Geld, das auf meinem Bankkonto spärliche Zinsen abwarf. Meine Sehnsucht nach ihrer Nähe verhinderte, dass ich auf Diebestour ging. Und meine Schüchternheit verhinderte, dass ich sie ansprach. Doch dann kam er, dieser Moment, auf den ich immer gewartet hatte – ganz plötzlich und alles nur, weil meine Blase brannte und ich dringend aufs Häuschen musste. Ich ging in einen Tea-Room gegenüber dem Haus, in dem sie gerade den Englischkurs besuchte. Als ich wieder die Treppe hochstieg, sah ich, wie sie sich an einen Tisch setzte – nicht an irgendeinen Tisch, nein, an jenen, an dem ich mich hingesetzt hatte. Der Tea-Room war eng und gut besucht. Ein Zufall also. Aber den wollte ich nutzen. Ich lächelte, setzte mich, sah aber gleich, dass sie nicht in Stimmung war, um mit mir zu reden. Sie zündete sich eine Zigarette an, hielt das Feuerzeug lange in ihrer linken Hand, inhalierte tief und wählte mit ihrem Mobiltelefon eine Nummer. Etwas bereitete mir Unbehagen bei ihrem Anblick. Ich wusste nur nicht, was es war. Sie war bezaubernd wie immer. Aber etwas störte mich. Ich versuchte, sie nicht anzustarren, was mir schwer fiel. Noch schwerer fiel es mir aber, sie anzusprechen. Schließlich sagte ich: „besetzt?“ und zeigte auf ihr Handy. Sie schaute mich wütend an. „Was geht dich das an, du Idiot?“ Die liebenswerteste Person, die mir je begegnet war, schmetterte all meine Gefühle mit einem Satz nieder, walzte durch mein Herz und schüttelte mich ab wie ein lästiges Insekt. Ich folgte ihr trotzdem. Sie ging zu ihrem Wagen, setzte sich hinters Steuer, fuhr jedoch nicht los. Ich sah, wie sie sich eine Zigarette anzündete. Erneut stutzte ich. Doch diesmal wurde mir klar, weshalb. Als sie losfuhr, gelang es mir, ihr in meinem Wagen zu folgen. Es wurde eine lange Reise durch die Nacht. Sie endete weit außerhalb der Stadt vor einem verfallenen, kleinen Haus an einem Waldrand. Ich schlich um das Haus und sah durch ein Fenster, wie sie in den Keller ging. Ich hörte erstickte Schreie aus dem Keller und spürte mein Herz laut und schnell pochen. Held wider Willen: Ich schlich nach unten. Dann sah ich sie. Sie war auf einem Eisenbett angekettet, den Mund mit einem Pflaster zugeklebt. Schön war sie, schön und voller Angst. Und neben ihr die böse Schwester, die Zwillingsschwester. Ich hörte ihre Stimme. Niemand vermisst dich, niemand vermisst die erfolgreiche Sabine – alle machen der erfolglosen Susanne den Hof. Ich habe es immer gewusst. Ich hörte meine eigene Stimme, ein bebendes Kreischen. „Ich vermisse sie, ich liebe sie.“ Die böse Schwester war wie gelähmt, ich hatte keine Mühe, sie zu überwältigen. In der Zeitung feierte man mich wie einen Helden. Doch meine große Liebe umarmte mich nur wie einen Lebensretter und netten Kerl. Geheiratet hat sie schließlich einen dieser braungebrannten Bankangestellten. Und ich besuche abends wieder Kurse für Erwachsene. Nie länger als zwei Minuten, ihr wisst schon, weshalb.
Nun die Frage:
Warum stutzt er, als er die Frau im Tea-Room sitzen sieht?
39 | Familientisch
Am Mittagstisch sitzen ein Großvater, eine Großmutter, zwei Väter, zwei Mütter, vier Kinder, drei Enkel, ein Bruder, zwei Schwestern, zwei Söhne, zwei Töchter, ein Schwiegervater, eine Schwiegermutter und eine Schwiegertochter.
Wie viele Teller werden mindestens benötigt?
38 | 12 Münzen - 2 Stapel
Dir werden beide Augen verbunden und es werden vor dir zwölf Euromünzen in eine Reihe gelegt. Sechs nebeneinanderliegende Münzen liegen mit dem Wappen nach oben, die anderen sechs nebeneinanderliegend mit der Zahl nach oben.
Die Reihenfolge kennst du nicht.
Du sollst nun die Euromünzen in zwei Haufen aufteilen, so dass in jedem Haufen genau gleich viele Münzen mit dem Wappen nach oben liegen.
Leider lässt sich durch Ertasten nicht herausfinden ob jeweils Wappen oder Zahl oben liegt.
Was musst du tun, nachdem du die Münzen in zwei Haufen aufgeteilt hast?
37 | Die zerbrochene Scheibe
Einer von vier Jugendlichen hat beim Fußballspielen eine Fensterscheibe zerlegt.
Der Hausmeister stellt die Vier zu rede, doch nur (genau) eine Person sagt die Wahrheit:
Max: Vanessa hat den Ball geschossen.
Tim: Ich war es nicht!
Vanessa: Rainer war es.
Rainer: Vanessa lügt!
Wer hat nun den Ball geschossen?
36 | Runder Tisch - gelogen wird, als gäb´s kein Morgen mehr
Einige dieser Leute sagen immer die Wahrheit, die anderen lügen immer.
Jeder am Tisch behauptet, dass sein linker Sitznachbar ein Lügner sei.
Und jeder behauptet zusätzlich, dass sein rechter Sitznachbar ebenfalls ein Lügner sei.Lore spricht in die Runde: „An diesem Tisch sitzen 15 Personen.“
Darauf erhebt sich Heinz und protestiert lautstark: „Du lügst ja. Hier sitzen im Moment genau 13 Personen.“
35 | Sinnvolle Wörter
Gesucht ist ein Wortende, welches mit folgenden Wortanfängen jeweils zusammen ein sinnvolles Wort ergibt:
B …………………………
Fl ………………………..
Sch ……………………..
Tr ……………………….
Z …………………………
Welches Wort-Ende wird gesucht?
34 | ... an der Weggabelung
Ein Wanderer will in die nächste Stadt und kommt an eine Weggabel. Dort sitzen am Wegrand 2 Männer. Der eine sagt immer die Wahrheit, der andere lügt immer. Der Wanderer kennt den Weg leider nicht.
Mit einer einzigen Frage gelingt es ihm herauszufinden, welcher der beiden Wege in die Stadt führt.
Welche Frage hat er an einen der am Wegrand sitzenden Männer gerichtet?
33 | Das Dreibein
Ein Zweibein sitzt auf einem Dreibein und isst ein Einbein.
Da kommt ein Vierbein und nimmt dem Zweibein das Einbein weg.
Da nimmt das Zweibein das Dreibein und schlägt das Vierbein.
Was ist das Dreibein?
32 | Gleichmäßig in Reihen
Ein Boulespieler will Übungskugeln für Schussübungen in gleichmäßige Reihen platzieren.
Als erstes versucht er es in Dreierreihen, doch es bleiben zwei Kugeln übrig.
Als nächstes versucht er es mit Viererreihen, und wieder bleiben zwei Kugeln übrig.
Mit der Fünferreihe klappt es schließlich.
Wie viele Kugeln hat der Boulespieler mindestens?
31 | Bittere Pille
Ein Mann geht zum Arzt und bekommt drei Tabletten, die er alle 30 Minuten einnehmen soll.
Wann nimmt er die letzte Tablette?
30 | Die Steigerung zu 29: In 4 Behälter liegen welche Kugeln?
Es gibt 4 Behälter. In jedem Behälter liegen 3 Kugeln.
In einem Behälter befinden sich drei weiße Kugeln, in einem zwei weiße und eine schwarze Kugel, in dem dritten eine weiße und zwei schwarze und in dem vierten Behälter drei schwarze Kugeln.
Die Behälter sind entsprechend beschildert (WWW, WWS, SSW, SSS), aber wiederum derart, dass die Schilder auf keinen Fall den Inhalt der einzelnen Behälter angeben.
Wie viele Kugeln muss man nun mindestens herausnehmen, bis eindeutig feststeht, welcher Behälter welche der vier Dreiersätze Kugeln enthält?
29 | Wo liegen welche Kugeln?
Es gibt 3 Behälter.
In jedem Behälter liegen 2 Kugeln.
In einem der Behälter liegen zwei weiße Kugeln, in dem anderen eine weiße und eine schwarze Kugel und im dritten liegen zwei schwarze Kugeln.
Die Behälter sind beschildert – auf dem einen Schild steht WW, auf dem anderen WS und auf dem dritten SS.
Aber jemand hat die Schilder so vertauscht, dass sie auf keinen Fall mehr den Inhalt der einzelnen Behälter angeben.
Man darf nun so lange nacheinander jeweils eine Kugel aus einem der Behälter nehmen (ohne hineinzuschauen!), bis eindeutig feststeht, welcher Behälter welche der drei Kugelpaare enthält.
Wie viele Kugeln muss man mindestens herausnehmen, um dieses Ziel zu erreichen?
28 | Mal ´ne einfache Buchstabenreihe
M D M D . . .
Welcher Buchstabe folgt in dieser Reihe?
27 | Wie kommen diese Preise zustande?
In einem Kleiderladen sind die Preise für Kleidungsstücke sehr seltsam ausgewiesen:
- Ein Hemd kostet 20 €
- eine Krawatte 40 €
- Socken 30 €
- ein Anzug nur 25 €
Was würde in diesem Kleiderladen wohl eine Unterhose kosten?
26 | Zeitmessung mal anders
Du musst eine Viertelstunde messen.
Für die Zeitmessung findest du zwei Zündschnüre, von denen du weißt, dass jede der beiden genau eine Stunde brennt.
Allerdings verbrennen diese nicht gleichmäßig.
Wenn die Hälfte einer Schnur verbrannt ist kannst du nicht davon ausgehen, dass genau eine halbe Stunde um ist.
Wie kannst du trotzdem genau eine Viertelstunde messen?
25 | Der fiese König
Vor langer Zeit herrschte ein König, der stets alle Gefangenen hinrichten ließ.
Um deren Schuld zu beweisen, hatte er eine kleine Schatulle mit einem weißen Elfenbein-Kügelchen und einem schwarzen Ebenholz-Kügelchen.
Jeder Gefangene durfte eines der beiden Kügelchen aus der Schatulle ziehen.
War’s das schwarze, so galt er als schuldig und wurde hingerichtet.
Zog er dagegen das weiße, so kam er frei.
Merkwürdigerweise gelang es aber nie jemandem, das weiße Kügelchen zu ziehen, und im ganzen Land flüsterte man sich bald zu: „Unser König, der Fiesling, hat zwei schwarze Kügelchen in seinem Kästchen.“ Doch niemald traute sich das laut zu sagen, und so zogen weiterhin alle Gefangenen das schwarze Kügelchen und wurden hingerichtet, bis eines Tages ein Gefangener die rettende Idee hatte.
Hinweis:
Er hatte keine Möglichkeit, ein Kügelchen zu färben oder zu vertauschen.
Er konnte auch nicht beide ziehen – hätte er gar keines gezogen, wäre er ebenfalls hingerichtet worden.
Wie konnte er sein Leben retten?
24 | Münzenrätsel: Das Dreieck
Drei sind einer zu wenig?! …

Erzeuge ein Dreieck mit einer nach unten zeigenden Spitze, du darfst dabei jedoch nur drei „Münzen“ bewegen.
Wie kriegst du das hin?
23 | ... noch eine Buchstabenreihe
M V E M J . . .
Welcher Buchstabe folgt als nächster in dieser Reihe?
22 | Buchstabenreihe
E Z D V F . . .
Welcher Buchstabe folgt als nächster in dieser Reihe?
21 | Die Fahrkarte
Eine Tageskarte in einen Bus kostet 1 Euro.
Ein Einzelfahrschein kostet 50 Cent.
Ein dem Busfahrer unbekannter Mann betritt den Bus, gibt dem Fahrer wortlos 1 Euro und bekommt dafür eine Tageskarte.
Hinweis: Der Mann hatte keine weiteren Personen dabei, verständigte sich nicht über Zeichen und fuhr zum ersten Mal mit diesem Bus.
Woher wusste der Busfahrer, dass der Mann eine Tageskarte (und keine Einzelkarte) wollte?
20 | Spieler sortieren
Ein Trainer stellt seiner Trainingsgruppe (24 Spieler) eine knifflige Aufgabe:
Jeder Spieler bekommt vom Trainer eine Schildkappe auf, entweder eine rote oder eine grüne. Da es aber Abend ist, sehen die Spieler im dunklen Bereich des Trainingsplatzes weder die Farbe ihrer eigenen Kappe, noch die Farben der anderen Spieler.
Die Spieler müssen jetzt folgende Aufgabe lösen:
Sie sollen den dunklen Bereich verlassen und sich im Scheinwerferlicht, nach Mützenfarbe gruppiert, aufstellen.
Die Spieler dürfen, solange sie im dunklen Platzbereich sind, beliebig miteinander reden und Pläne schmieden – die Kappenfarben sind natürlich hier noch immer für niemanden erkennbar.
Sobald sie den Bereich der Scheinwerfer betreten, kann jeder Spieler die Mützen der anderen sehen, nicht aber seine eigene. (Die Mützen dürfen natürlich nicht abgenommen werden.)
Sobald es im Scheinwerferlicht hell genug ist, dass sie die Farben der Mützen erkennen können, dürfen sie nicht mehr miteinander kommunizieren, weder verbal noch durch Zeichen noch sonstwie.
(Es sind auch keine Tricks erlaubt, dieses Kommunikationsverbot irgendwie zu umgehen.)
19 | ... mal eine Wortsuche
Was ist größer als Gott?
Was können sich reiche Leute nicht leisten?
Was haben die armen Leute?
Woran stirbt man, wenn man es andauernd isst?
Wie lautet das gesuchte Wort?
18 | Silberfarbene, dunkle und schwarze Kugeln
Beim abendlichen Boule-Training sollen als Zielkugeln unterschiedliche Kugelfarben zum Einsatz kommen. Der Trainer schickt einen Spieler in den Geräteraum, um schnell noch drei silberfarbene Kugeln zu holen – „Die Übungskugeln liegen im Eimer, der rechts in der Ecke steht“.
Im Geräteraum ist es allerdings stockfinster. Der Spieler kann im Dunkeln nicht unterscheiden, welche Farbe eine Kugel in seiner Hand hat. Er weiß aber, dass im Schrank genau 11 silberfarbene, fünf dunkle und zwei schwarze Kugeln liegen. Vorsichtig tastet er sich zum Eimer vor.
Wie viele Kugeln muss er mindestens mit raus nehmen, damit auf jeden Fall drei silberfarbene Kugeln mit dabei sind?
17 | Zahlenreihe
Und wieder geht es um die Fortführung einer Zahlenreihe:
33 – 31 – 39 – 37 – 43 – 41 – 45 – 43 – …
Wie lautet die nächste Zahl in dieser Reihe?
16 | Aufeinandertreffen in der Wüste
In einer Wüste treffen zwei Karawanen aufeinander.
Die Führer der beiden Karawanen unterhalten sich freundschaftlich.
Ein Karawanenführer sagt zum anderen: „Wenn du mir ein Kamel abgibst, dann haben wir gleichviele.“ Da erwidert der andere: „Wenn du mir ein Kamel abgibst, dann habe ich doppelt so viele wie du.“
15 | Logik ohne Zahlen
Diese Buchstabenreihe soll um einen Buchstaben ergänzt werden.
Finde also eine „logische“ Erweiterung der Reihe:
P R F E O …
Um welchen Buchstaben muß die Reihe erweitert werden?
14 | Die Sache mit den Sanduhren
Du hast zum Essen geladen.
Damit die Nudeln „al dente“ sind, sollen sie genau 5 Minuten kochen.
Du suchst, aber kannst keine anderen Uhren finden, als 2 Sanduhren:
Die erste braucht genau 4 Minuten um ganz durchzulaufen, die zweite exakt 3 Minuten.
Nicht ganz optimal, um die genaue Kochzeit von 5 Minuten einzuhalten.
Wie kannst du trotzdem mit Hilfe dieser beiden Sanduhren die Garzeit abmessen?
13 | Wo ist hier die Logik?
8 | 3 | 1 | 11 | 5 | 9 | 6 | 7 | 4 | 10 | 2 | 12
Nach welchem Prinzip ist Zahlenreihe geordnet?
12 | Umstellen
Jedes der folgenden Wörter ist durch Umstellung der Buchstaben in ein neues zu verwandeln.
Die Anfangsbuchstaben der neuen Wörter ergeben ein Sprichwort.
Nelke – Angel – Neider – Robe – Belag – Rune – Falte – Selma – Ampel – Blei – Hasenbein – Bilse – Rang – Braun – Gurt
Welches Sprichwort wird gesucht?
11 | Dem Tod entronnen
Ein Gefangener wird zum Tod verurteilt.
Er darf mit einer Aussage zwischen Hängen und Köpfen wählen: Bei einer falschen Aussage, würde er geköpft. Ist die Aussage richtig, so endet er am Galgen.
Nach kurzer Überlegung macht der Todeskandidat dann eine Aussage. Nun kann er weder erhängt noch geköpft werden.
Welche Aussage hat den Verurteilten vor dem Tod bewahrt?
10 | Ganz einfach so eine Passwortkombination
Ein Unhold will sich in die Stadt einschmuggeln.
Am Stadttor wacht allerdings ein gewitzter Torwächter, an dem er nicht so einfach vorbei kommt.
Er legt sich zunächst mal in Hörweite auf die Lauer und beobachtet, wie andere das Tor passieren.
Ihm wird schnell klar: Er braucht ein Passierwort.
Als erstes kommt ein dicker Mönch.
Der Torwächter sagt:“16?“, worauf der Mönch schlicht:“8!“ sagt.
Dann kommt ein Bauer.
Der Torwächter sagt:“28?“ und der Bauer:“14!“.
Als ein Händler kommt,
sagt der Wächter:“8?“ und bekommt als Antwort:“4!“.
Alle dürfen passieren.
„Nun ja, das ist ja einfach!“ denkt der Spion.
Auf die Frage des Torwächters:“12?“ antwortet er lässig „6!“ – und wird umgehend verhaftet.
Was hätte er wohl sagen müssen?
09 | Die Säcke mit den Münzen - und wieder das Gewicht ...
10 Säcke mit sind mit Münzen gefüllt.
Die Säcke sind von 1 bis 10 durchnummeriert.
9 Säcke sind mit 10g-Münzen gefüllt und ein Sack mit 9g-Münzen.
Zur Verfügung steht eine Digitalwaage, mit der man einmal wiegen darf.
Wie kann man bestimmen, in welchem Sack die 9g-Münzen sind?
08 | Die Sache mit dem Gewicht der Pétanque-Kugeln
Du hast 3 Sätze Pétanque-Kugeln gekauft: Gleiches Aussehen und gleiches Gewicht.
Der Verkäufer meldet sich bei dir, um dir mitzuteilen, dass eine der Kugeln anscheinend vertauscht wurde und du nun leider acht Kugeln mit gleichem Gewicht und eine neunte Kugel mit mehr Gewicht im Gepäck hast.
Du hast lediglich eine Balkenwaage zur Verfügung und musst mit maximal 2 Wiegungen herauszufinden, welche die falsche (schwerere) Kugel ist.
Wie gehst du vor?
07 | Messbecher und doch kein Maß
Du hast einen 3-Liter Behälter und einen 5-Liter Behälter zur Verfügung.
Beide Behälter haben keine Maßangaben.
Du brauchst allerdings exakt 4 Liter Milch.
Wie ist dies mit den beiden Behältern machbar?
06 | Laterale, Texträtsel | Zu spät
Laterale werden auch Mini-Misteries oder Ja-Nein-Rätsel genannt.
Es handelt sich um sehr kurze (vermeintlich mysteriöse) Geschichten, die scheinbar gar nicht sein können, oder zumindest keinen Sinn machen.
Trotzdem gibt es eine logische Erklärung: Wer findet diese logische Erklärung?
Um sich das Leben zu nehmen, springt ein Mann von einem 10-stöckigen Hochhaus.
Während er in den Abgrund fliegt, hört er aus irgendeinem Stockwerk ein Telefon klingeln.
Warum bereut er in diesem Moment seinen Entschluß?
05 | Kreuz und Quer

Die 9 Punkte (3 mal 3 Punkte – siehe Skizze) sollen mit nur geraden Linien verbunden werden, ohne den Stift abzusetzen.
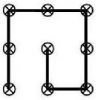
Im 2. Bild wurde die Aufgabe mit 5 Linien gelöst.
Wie muss das Bild aussehen, wenn nur 4 gerade Linien gezeichnet werden dürfen?
04 | Laterale, Texträtsel | Tod am Fenster
Laterale werden auch Mini-Misteries oder Ja-Nein-Rätsel genannt.
Es handelt sich um sehr kurze (vermeintlich mysteriöse) Geschichten, die scheinbar gar nicht sein können, oder zumindest keinen Sinn machen.
Trotzdem gibt es eine logische Erklärung: Wer findet diese logische Erklärung?
Ein Mann schaute aus dem Fenster und beobachtete eine hübsche Frau, die gerade an seinem Haus vorbei ging.
Kurz danach war er tot.
Hätte er die Frau nicht beobachtet, würde er vielleicht noch leben.
Er ist aber nicht aus dem Fenster gestürzt.
Was ist passiert?
Tipp:
Es gibt eine logische Erklärung – allerdings sollte man nicht nur das „Offensichtliche/Eigentlich zu Erwartende“ sehen.
03 | Wo bin ich?
2 Ortschaften liegen genau nebeneinander: Lügenhausen und Wahrhausen.
Die Einwohner von Lügenhausen sind allesamt Lügner, die von Wahrhausen sagen grundsätzlich die Wahrheit.
Du hast dich in der Gegend verlaufen und bist dir auch nach Studium der Landkarte nicht sicher, ob du dich in Lügenhausen oder Wahrhausen befindest.
Welche Frage musst du einer beliebigen Person auf der Straße stellen um anschließend eindeutig zu wissen in welcher der beiden Ortschaften du bist?
Tipp:
Die Frage besteht lediglich aus 3 Wörtern.
02 | Die Expedition ohne Lampe
An alles wurde gedacht, als die Expedition vorbereitet wurde:
Vorräte, Zelte, Trinkwasser, Waffen, …
Was nach ein paar Expeditionstagen zum Problem wurde:
Der Docht in der mitgenommenen Petroleumlampe so weit verbraucht, dass er sich nicht mehr ins Petroleum eintauchen ließ. Es war auch kein Petroleum mehr zum Nachfüllen dabei. Zwar war in der Lampe noch genügend Petroleum drin, aber der Docht reichte nicht mehr so weit nach unten, dass er sich mit dem Brennstoff vollsaugen konnte.
Welchen Trick wandten die Expeditionsteilnehmer an, damit ihre Lampe weiterhin brennen konnte?
01 | Zahlenfolge
1
11
21
1211
111221
Wie lautet die nächste Zeile?
Tipp:
Es hat nichts zu bedeuten, wie die Ziffern übereinander angeordnet sind. Die meisten Leute können das Rätsel nicht lösen, weil sie viel zu kompliziert denken. Es ist aber sehr viel einfacher als man denkt. Man muss nicht einmal rechnen.
Jeder der bis drei zählen kann, kann auch dieses Rätsel lösen.
Die Lösungen zu den Denk- und Knobelaufgaben
Noch einmal der Apell
Geht nicht gleich den (vermeintlich) einfachsten Weg und schaut (bequem/feige) nach den Lösungen, die euch angeboten werden und natürlich die eigene (Kopf-)Arbeit der Lösungssuche abnehmen würden.
Verlasst euch auf eure eigenen Fähigkeiten, konzentriert euch und gebt nicht auf.
Wenn´s nur der Blick in die Lösungen zur eigenen Kontrolle ist, dann soll´s recht sein – aber ihr werdet euch ärgern, wenn ihr schon nachschaut, bevor ihr mit eurem eigenen Gehirn die Aufgabe gemeistert habt?!
Lösung zu 47 | Wachsverschwendung beim jährlichen Adventskranz
Addiert man die Kerzenstunden aller vier Sonntage, kommt man auf 1+2+3+4=10 Stunden.
Der Sparfuchs braucht also Wachs für 10 Stunden – und das sind genau 250 Gramm
(Denn in einer Stunde verbrennen 25 Gramm).
Lösung zu 46 | Ganz schön verdreht
Die gesuchte Zahl lautet:
87
Erklärung:
Einfach die Zahlen auf ein Papier schreiben und dann das Blatt drehen (auf dem Kopf lesen):
86 – X (87) – 88 – 89
Lösung zu 45 | Welche Zahl ist gesucht?
Die gesuchte Zahl lautet: 3
2580 = 3
Erklärung:
Wenn kleine Kinder einen Kugelschreiber in der Hand haben, malen sie gerne die Kreise in den geschlossenen Bereichen der Zahlen aus. Die Anzahl dieser Kreise steht jeweils auf der rechten Seite!
Kleine Kinder lösen die Aufgabe daher häufig schneller als Erwachsene.
Lösung zu 44 | Was für eine Frage?
Die richtige Frage lautet:
„Wirst du mir mit „nein“ antworten?“
Lösung zu 43 | Rätselhafte Addition - Buchstaben ersetzen
9 5 6 7
+ 1 0 8 5
———-
1 0 6 5 2
Und hier noch die Lösung für die weitere Buchstaben-Addition:
29786
+ 850
+ 850
——-
31486
Lösung zu 42 | Welches Wort passt nicht?
Die Lösungsbuchstaben ergeben in der Reihenfolge 1 – 7 ein Wort:
TECHNIK
Lösung zu 41 | Das Verwandtschaftsproblem
Die Mutter der Frau muss verheiratet sein, sonst hätte sie keine Schwiegermutter. Die Mutter des Mannes ist diese Schwiegermutter. Nun gibt es zwei Möglichkeiten:
1. Die Mutter der Frau ist mit dem Mann verheiratet. Der Mann ist also der Vater der Frau, sie folglich seine Tochter.
2. Die Mutter der Frau ist mit dem Mann verschwägert. Der Mann ist also der Onkel der Frau, sie folglich seine Nichte.
Denkbar wäre auch, dass der Mann der Stiefvater der Frau ist, also nicht der leibliche Vater. Die Frau wäre dann seine Stieftochter.
Vermutlich gibt es noch exotischere Konstruktionen, auf die die Bedingungen des Verwandtschaftsproblems zutreffen…
Lösung zu 40 | Warum stutzt er, als er die Frau im Tea Room sieht?
Er stutzt weil sie das Feuerzeug in der linken Hand hat und folglich mit rechts das Mobiltelefon wählt, also Rechtshänderin ist.
Auf dem Foto hatte die Frau in der linken Hand eine Zigarette, ist folglich Linkshänderin.
Lösung zu 39 | 12 Münzen - 2 Stapel
Du bildest zuerst zwei Haufen mit jeweils sechs Münzen.
Dadurch erreichst du, dass in dem einen Haufen genau so viele Münzen das Wappen zeigen, wie in dem anderen Haufen die Zahl.
Nun drehst du alle Münzen eines Stapels um.
Lösung zu 38 | Familientisch
Großvater (Vater vom Vater / Schwiegervater der Mutter)
Großmutter (Mutter vom Vater / Schwiegermutter der Mutter)
Vater (Sohn vom Großvater / Kind)
Mutter (Schwiegertochter)
Kind (Sohn des Vaters / Enkel vom Großvater / Bruder seiner Schwestern)
Kind (Tochter des Vaters / Enkel vom Großvater / Schwester ihres Bruders)
Kind (Tochter des Vaters / Enkel vom Großvater / Schwester ihres Bruders)
Also werden mindestens 7 Teller benötigt.
Lösung zu 37 | Die zerbrochene Scheibe
Wenn nur eine der Aussagen stimmt, dann gilt folgendes:
Wenn es Max war, dann sagen Tim und Rainer die Wahrheit.
Wenn es Vannessa war, dann sagen Max, Tim und Rainer die Wahrheit.
Wenn es Rainer war, dann sagen Tim und Vanessa die Wahrheit.
Wenn es Tim war, dann sagt nur Rainer die Warheit.
Also war es Tim.
Lösung zu 36 | Runder Tisch - gelogen wird ...
Heinz hat recht, aber nur weil er selbst aufgestanden ist.
Am Tisch befinden sich 14 Personen.
Weil jeder seine zwei Nachbarn der Lüge bezichtigt, muss immer ein Lügner neben einem sitzen, der die Wahrheit sagt.
Daher ist insgesamt eine gerade Anzahl von Personen am Tisch.
Lore Lügt also.
Da Heinz sie der Lüge bezichtigt, sagt er die Wahrheit.
Lösung zu 35 | Sinnvolle Wörter
Gesucht ist die Endung „aum“.
Lösung zu 34 | ... an der Weggabelung
Der Wanderer hat seine Frage so formuliert, dass er beide Männer gleichermaßen mit einbezieht.
Er fragt einen beliebigen Mann: „Was würde der Andere mir sagen, wenn ich fragen würde, welcher Weg zur Stadt führt?“.
Als Antwort hat er auf jeden Fall eine Lüge erhalten – und daher den anderen Weg gewählt.
Lösung zu 33 | Das Dreibein
Das Einbein ist ein Hühnerschenkel,
das Zweibein ein Mensch,
das Dreibein ein Hocker
und der Vierbeiner ein Hund.
Lösung zu 32 | Gleichmäßig in Reihen
Die gesuchte Zahl ist gerade und durch 5 teilbar. Somit ist sie durch 10 Teilbar. Nun suchen wir eine Zahl, die um zwei kleiner ist und sowohl durch drei und durch vier teilbar ist. Also die kleinste Zahl, die mit einer 8 endet und durch 12 teilbar ist. Das ist die 48. Also müssen es mindestens 50 Kugeln sein. Die nächstmöglichen Lösungen wären 110 und 170.
Lösung zu 31 | Bittere Pille
Gar nicht so schwer:
Die erste Pille nimmt der Mann sofort zu sich, die zweite nach 30 Minuten und die letze nach einer Stunde.
Lösung zu 30 | Die Steigerung: 4 Behälter - welche Kugeln?
Es genügt im besten Fall, drei Kugeln zu ziehen:
Man zieht zuerst zwei Kugeln aus Behälter 2:
– Sind beide weiß, so sind in Behälter 2 ausschließlich weiße Kugeln. Man zieht dann die dritte Kugel aus Behälter 3. Ist diese weiß, so müssen sich in Behälter 3 zwei weiße und eine schwarze Kugel befinden, in Behälter 1 folglich die drei schwarzen und in Behälter 4 daher eine weiße und zwei schwarze Kugeln.
Ist die dritte gezogene Kugel aus Behälter 3 schwarz, so muss man noch mindestens eine vierte Kugel (aus Behälter 3) ziehen.
– Zieht man eine weiße und eine schwarze Kugel aus Behälter 2, dann befinden sich in Behälter 2 eine weiße und zwei schwarze Kugeln. Man kann dann z.B. aus Behälter 4 die dritte Kugel ziehen. Ist sie schwarz, so muss Behälter 4 zwei weiße und eine schwarze enthalten, Behälter 1 folglich die drei schwarzen und Behälter 3 die drei weißen enthalten.
In allen andern (bis auf die Symmetriefälle der genannten Fälle) muss man mehr als drei Kugeln ziehen.
Lösung zu 29 | Wo sind welche Kugeln?
Wenn sich nur zwei Kugeln in den Behältern befinden, so ist die Lösung einfach:
Man muss nur eine Kugel aus dem mit WS beschilderten Behälter nehmen.
Ist die Kugel weiß, so befinden sich in diesem Behälter die beiden weißen,
in dem mit WW beschilderten Behälter die beiden schwarzen Kugeln
und folglich in dem mit SS beschilderten Behälter eine schwarze und eine weiße Kugel.
Ist die gezogene Kugel schwarz, so befinden sich in diesem Behälter die beiden schwarzen,
in dem mit SS beschilderten Behälter die beiden weißen Kugeln
und folglich in dem mit WW beschilderten Behälter eine schwarze und eine weiße Kugel.
Lösung zu 28 | Mal ´ne einfache Buchstabenreihe
Wirklich ganz einfach:
Montag, Dienstag, Mittwoch, Donnerstg, Freitag, …
Lösung zu 27 | Wie kommen diese Preise zustande?
Jeder Buchstabe eines Kleidungsstücks kostet hier 5 €.
Es kostet daher:
Ein Hemd mit 4 Buchstaben 20 €,
eine Krawatte mit 8 Buchstaben 40 €,
…
Demnach kostet eine Unterhose mit 9 Buchtaben 45 €!
Lösung zu 26 | Zeitmessung mal anders
Zünde eine Zündschnur an beiden Enden an, die andere nur an einem.
Wenn die erste Zündschnur abgebrannt ist brennt die andere noch eine halbe Stunde.
Diese Zeit verkürzt du um die Hälfte indem du sie auch noch an der anderen Seite anzündest.
So kommst du dann auf die erwünschte Viertelstunde.
Lösung zu 25 | Der fiese König
Da immer das schwarze Kügelchen gezogen wurde, musste er davon ausgehen, dass tatsächlich beide schwarz waren, wodurch er gar keine Chance hatte, das weiße zu ziehen.
Er zog daher eines der Kügelchen und verschluckte es schnell, bevor jemand die Farbe sehen konnte.
Somit konnte man nur nachschauen, welches Kügelchen noch in der Schatulle war, und dieses war natürlich schwarz.
Die gezogene Kugel musste somit die weiße gewesen sein.
Der König konnte nun auch nicht sagen, dass die andere Kugel ebenfalls schwarz war, denn damit hätte er sich ja selbst verraten.
Lösung zu 24 | Münzenrätsel: Das Dreieck

Lösung zu 23 | ... noch eine Buchstabenreihe
Merkur, Venus, Erde, Mars, Jupiter, Saturn, …
Lösung zu 22 | Buchstabenreihe
Eins, Zwei, Drei, Vier, Fünf, Sechs, …
Lösung zu 21 | Die Fahrkarte
Der Fahrgast hat in kleinen Münzen gezahlt, so dass er die 50 Cent auch hätte passen bezahlen können.
Lösung zu 20 | Spieler sortieren
Die Spieler können sich im Scheinwerferlicht beim Aufstellen sortieren:
Die ersten zwei Spieler stellen sich nebeneinander.
Jeder weitere Spieler sortiert sich nun so in die Reihe ein, dass er immer zwischen denen mit dem roten und denen mit den grünen Mützen steht.
Nach dieser Methode ist es egal, welche Farbe der hinzukommende Spieler selbst trägt.
Lösung zu 19 | ... mal eine Wortsuche
Das gesuchte Wort heißt „Nichts“!
Einfach, oder …?!
Lösung zu 18 | Silberfarbene, dunkle und schwarze Kugeln
Der Spieler muss natürlich 10 Kugeln holen um sicher zu gehen.
Bei nur 7 (oder gar weniger) Kugeln wäre es möglich, dass alle Kugeln dunkel und (oder) schwarz sind, aber dabei eben keine 3 silberfarbene Kugeln dabei sind.
Lösung zu 17 | Zahlenreihe
45 ist die gesuchte nächste Zahl.
Die Folge lautet
33 (-2) 31 (+8) 39 (-2) 37 (+6) 43 (-2) 41 (+4) 45 (-2) 43 (+2) 45
Lösung zu 16 | Aufeinandertrefen in der Wüste
Mathematische Formel:
Kamele des ersten Karawanenführers = a
Kamele des zweiten Karawanenführers = b
b-1 = a+1
b = a +2
b+1 = 2 * (a-1)
a+2+1 = 2* (a-1)
a +3 = 2a-2
3+2 = a
5 = a
Karawane 1 hat also demnach 5 Kamele und Karawane 2 hat 7 Kamele.
Lösung zu 15 | Logik ohne Zahlen
Der 2. und der 4. Buchstabe haben einen Strich mehr als der jeweils vorherige Buchstabe.
Dementsprechend ist die Lösung der Buchstabe Q.
Lösung zu 14 | Die Sache mit den Sanduhren
- Du drehst zunächst beide Uhren gleichzeitig um
- Du wartest bis die 3-Minuten-Uhr abgelaufen ist
- Diese drehst du sofort wieder um
- Wenn die 4-Minuten-Uhr durchgelaufen ist, ist in der 3-Minuten Uhr Sand von genau einer Minute
- Diese Uhr drehst du nochmals um.
- Wenn der Sand wieder zurückgelaufen ist, sind exakt fünf Minuten um.
Lösung zu 13 | Wo ist hier die Logik?
Die Reihenfolge ist lediglich alphabetisch sortiert:
Acht | Drei | Eins | …
Lösung zu 12 | Umstellen
Enkel – Nagel – Diener – Ebro – Gabel – Urne – Tafel – Amsel – Lampe – Leib – Eisenbahn – Silbe – Garn – Urban – Trug
= ENDE GUT ALLES GUT
Lösung zu 11 | Dem Tod entronnen
Er sagt: „Ich werde geköpft werden.“
Hätte man ihn anschließend tatsächlich geköpft, so wäre die Aussage richtig gewesen; nach der Vereinbarung jedoch hätte man ihn ja dann aber hängen müssen.
Hätte man ihn nach der Aussage gehängt, so wäre seine Aussage falsch gewesen. Aufgrund der Vereinbarung hätte man ihn dann Köpfen müssen.
Es war also mit dieser Aussage unmöglich, ihn noch hinzurichten!
Lösung zu 10 | Ganz einfach so eine Passwortkombination
- 16 wird mit 8 Buchstaben geschrieben.
- 28 wird mit 14 Buchstaben geschrieben.
- 8 wird mit 4 Buchstaben geschrieben.
- usw.
- 12 wird mit 5 Buchstaben geschrieben: Er hätte demnach 5 sagen müssen!
Lösung zu 09 | Die Säcke mit den Münzen - und wieder das Gewicht ...
- Nimm von Sack 1 eine Münze, von Sack 2 zwei Münzen usw.
- Nun liegen 55 Münzen auf der Waage
- Wären in jedem Sack 10g-Münzen, würde die Waage 550g anzeigen.
- 550 minus der gewogenen Gramm ergibt die Nummer des gesuchten Sacks
Beispiel:
Wären die 9g-Münzen in Sack 2, würde die Waage 532g anzeigen
(550g – 532g = 18g = 2mal 9g-Münzen aus Sack 2)
Lösung zu 08 | Die Sache mit dem Gewicht der Pétanque-Kugeln
- Lege auf jede Seite 3 Kugeln.
- Ist nun eine Seite schwerer, so ist die gesuchte Kugel dort. Ansonsten ist sie bei den dreien neben der Waage.
- Nun hat man nur noch drei Kugeln zur Auswahl.
- Zwei von diesen wiegt man.
- Ist eine der beiden schwerer, hat man die gesuchte Kugel. Ansonsten ist es die übrig gebliebene Kugel.
Lösung zu 07 | Messbecher und doch kein Maß
Die einfachste (nicht die einzige) Lösung:
- Den 5-Liter Behälter füllen.
- Diesen in den 3-Liter Behälter umfüllen – dadurch verbleiben 2 Liter im 5-Liter Behälter.
- Den 3-Liter Behälter leeren.
- Den Rest (2 Liter) aus dem 5-Liter Behälter in den 3-Liter Behälter kippen.
- Noch einmal den 5-Liter Behälter füllen und in den 3-Liter Behälter gießen, bis dieser voll ist.
- Nun sind genau 4 Liter im 5-Liter Behälter. Fertig!
Lösung zu 06 | Zu spät
Nach einem Atomkrieg ging er davon aus, er sei der einzige Überlebende und nun allein auf dieser Welt.
Lösung zu 05 | Kreuz und Quer
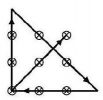
Lösung zu 04 | Tod am Fenster
Der Mann fuhr in seinem Auto die Straße vor seinem Haus entlang, als er durch das Seitenfenster die hübsche Frau sah, die ihn so sehr ablenkte, dass er einen Unfall verursachte.
Lösung zu 03 | Wo bin ich?
Die Frage lautet: „Wohnst Du hier?“
In Lügenhausen bekommt man auf diese Frage grundsätzlich „Nein!“ als Antwort, in Wahrhausen dagegen immer „Ja“!“.
Lösung zu 02 | Die Expedition ohne Lampe
Sie füllten zusätzlich Wasser in die Lampe.
Öl und Wasser vermischen sich nicht.
Das noch vorhandene Petroleum war leichter und schwamm über dem Wasser.
Lösung zu 01 | Zahlenfolge
In der ersten Zeile steht: 1 – Das ist 1-mal die 1.
Die nächste Zeile darum: 11 – Das ist 2-mal die 1.
Die nächste Zeile darum: 21 – Das ist 1-mal die 2 und 1-mal die 1.
Die nächste Zeile darum: 1211 – Das ist 1-mal die 1, 1-mal die 2 und nochmal 2-mal die 1.
Die nächste Zeile darum: 111221 – Das ist 3-mal die 1, 2-mal die 2 und nochmal 1-mal die 1.
Die gesuchte Zeile darum: 312211

